Лекция 1

Комплексные числа

Напомним, что комплексные числа можно определить как множество упорядоченных пар вещественных чисел $$ \mathbb C = \{(x,y) : x,y\in\mathbb R \}, \quad z=x+iy, $$ где $i$ --- мнимая единица ($i^2 = -1$). Действительная часть $\operatorname{Re} z = x$, мнимая часть $\operatorname{Im} z = y$. Множество $\mathbb C$ снабжено операцией сложения $$ z_1 + z_2 = (x_1+x_2) + i(y_1+y_2) $$ и операцией умножения $$ z_1\cdot z_2 = (x_1x_2-y_1y_2) + i(x_1y_2 + y_1x_2). $$ Для каждого числа $z\in\mathbb C$ существует противоположное по сложению число $-z$ такое, что $z+(-z) = 0$. Для каждого числа $z\ne 0$ существует обратное по умножению число $\dfrac{1}{z}$ такое, что $z\cdot\dfrac{1}{z} = 1$. Имеет место формула $$ \frac{1}{z} = \frac{x}{x^2+y^2} - i\frac{y}{x^2+y^2}. $$ Модуль числа $z=x+iy$ определяется как \begin{equation*}%\label{eq:modulz} |z| = \sqrt{x^2+y^2}. \end{equation*} Для модуля комплексного числа выполняются следующие свойства: \begin{equation} \begin{aligned} & |z|=0 \quad \Leftrightarrow \quad z=0;\\ & |z_1\cdot z_2|= |z_1|\cdot|z_2|, \quad |z^n| = |z|^n;\\ &\left|\frac{z_1}{z_2}\right| = \frac{|z_1|}{|z_2|}, \quad \text{ при } z_2\ne0;\\ & |\operatorname{Re} z|\leq |z| \text{ и } |\operatorname{Im} z|\leq |z|, \qquad(|x|\leq |z| \text{ и } |y|\leq |z|);\\ & |z|\leq |\operatorname{Re} z| + |\operatorname{Im} z|, \qquad (|z|\leq |x| + |y|);\\ & |z_1+z_2|\leq |z_1| + |z_2|\qquad \text{(неравенство треугольника);} \\ & ||z_1|-|z_2|| \leq |z_1-z_2|. \end{aligned} \end{equation} Число $\bar{z} = x-iy$ называется сопряжённым, к $z=x+iy$. При этом справедливы следующие свойства: \begin{equation*} \begin{aligned} & \overline{(z_1+z_2)} = \bar z_1 + \bar z_2;\\ & \overline{z_1\cdot z_2} =\bar z_1\cdot\bar z_2;\\ & \overline{\left(\frac{z_1}{z_2}\right)} = \frac{\bar z_1}{\bar z_2};\\ & \overline{\overline{z}} = z;\\ & z\cdot\bar z =\left(\operatorname{Re} z\right)^2 + \left(\operatorname{Im} z\right)^2, \quad (z\cdot\bar z = x^2+y^2);\\ & z\cdot\bar z = |z|^2, \quad |z| = \sqrt{z\cdot\bar z};\\ %& z = \bar z \quad \Leftrightarrow \quad \operatorname{Im} z =0;\\ & z+\bar z = 2\operatorname{Re} z \quad \text{ и } \quad z-\bar z = 2i\operatorname{Im} z;\\ \end{aligned} \end{equation*} Особо отметим следующее свойство \begin{equation}\label{eq:zbarz} z\cdot\bar z = (x+iy)\cdot(x-iy) = x^2+y^2 = |z|^2. \end{equation}

Комплексная плоскость

Рассмотрим плоскость и прямоугольную систему координат на ней. Ось абсцисс обозначим $\operatorname{Re} z$ и будем называть действительной осью, а ось ординат обозначим $\operatorname{Im} z$, будем называть мнимой осью. Каждому комплексному числу $z=x+iy$ сопоставим точку на этой плоскости с координатами $(x,y)$, и, другими словами, радиус-вектор с координатами $(x,y)$.

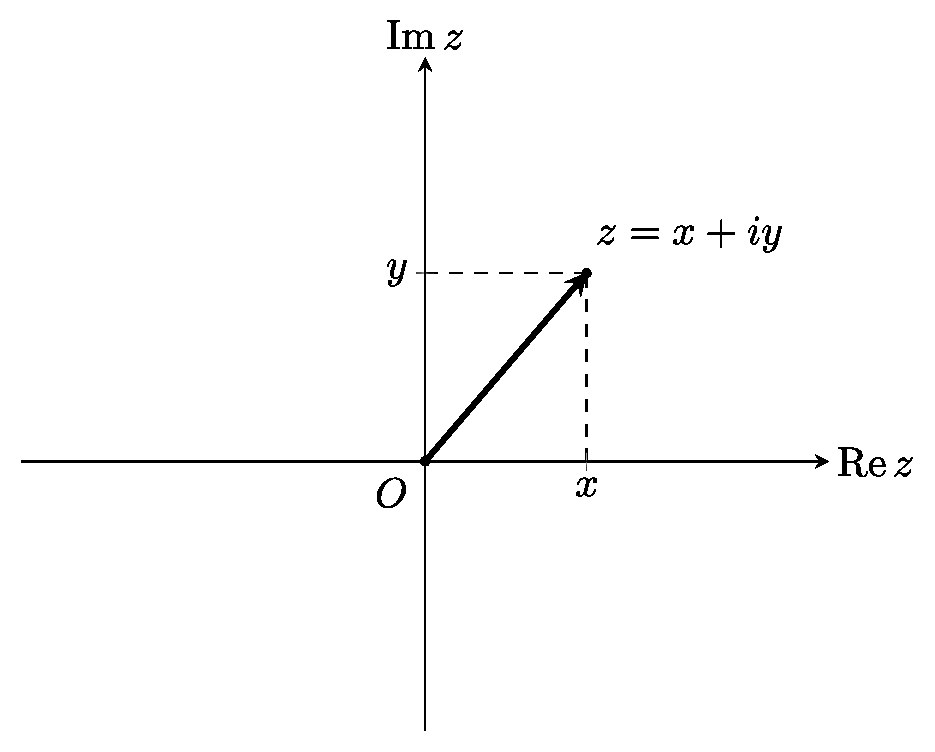
Заметим, что соответствие между комплексными числами и точками на комплесной плоскости является взаимнооднозначным соответствием (а в случае с вещественными числами, соответствие строится с точкам на вещественной прямой).

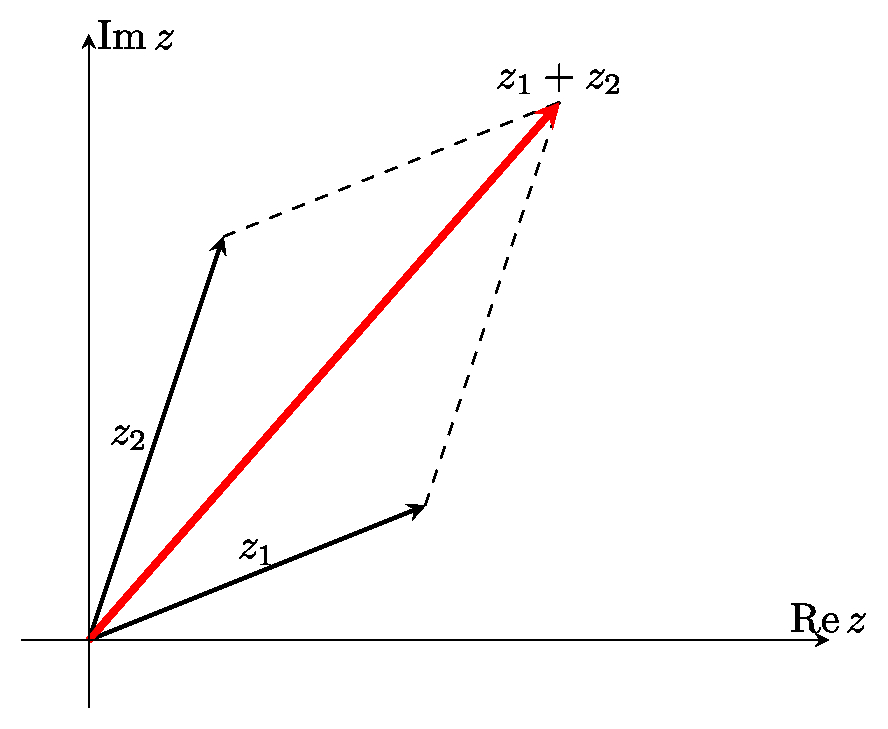
Геометрически сложение чисел $z_1$ и $z_2$ производится по правилу сложения векторов (по правилу параллелограмма).

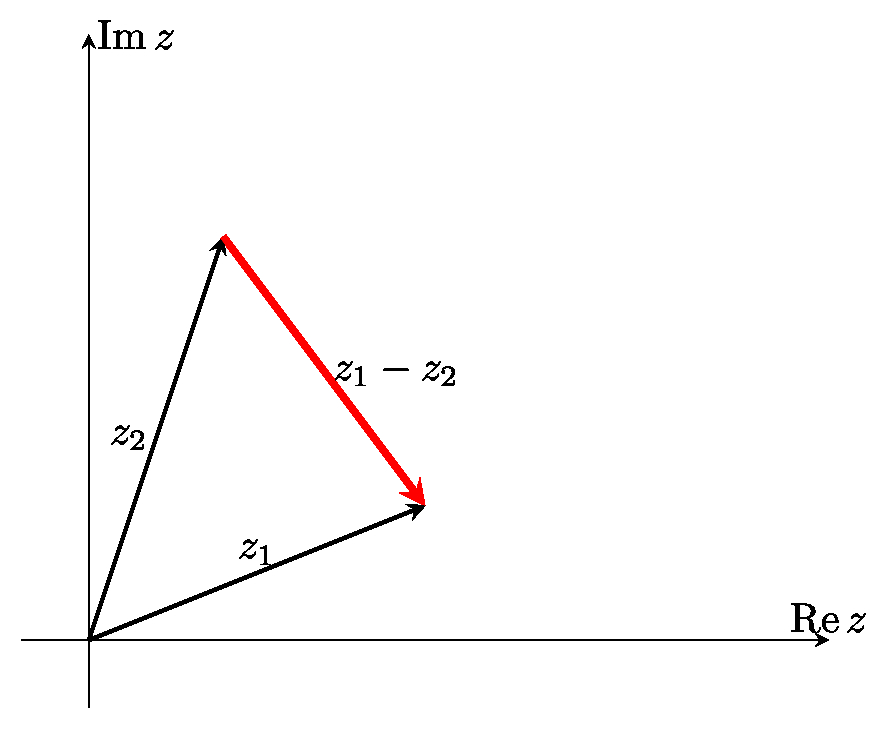
Разность $z_1-z_2$ представляется вектором, конец которого находится в точке $z_1$, а начало - в точке $z_2$.

Комплексным сопряжением числа $z$ на комплексной плоскости является вектор, симметричный вектору $z$, относительно оси абсцисс.

Модуль комплексного числа $z=x+iy$ равен длине вектора, соответствующего данному числу на комплексной плоскости, $$|z|= \sqrt{x^2+y^2}.$$ Несложно проверить, что расстояние между двумя точками комплексной плоскости $z_1$ и $z_2$ равно $|z_1-z_2|$. То есть, модуль разности двух комплексных чисел есть расстояние между точками на комплексной плоскости, которым соответствуют этим числам.

Полярные координаты

Любой вектор на плоскости полностью определяется своей длиной и углом с положительным направлением оси $Ox$. Модуль комплексного числа $$ \rho = |z| = \sqrt{x^2 + y^2} $$ это длина вектора $(x,y)$. Обозначим $\varphi = \operatorname{Arg} z$ - аргумент комплексного числа $z$, при этом $$ x = \rho\cos\varphi, \qquad y = \rho\sin\varphi. $$

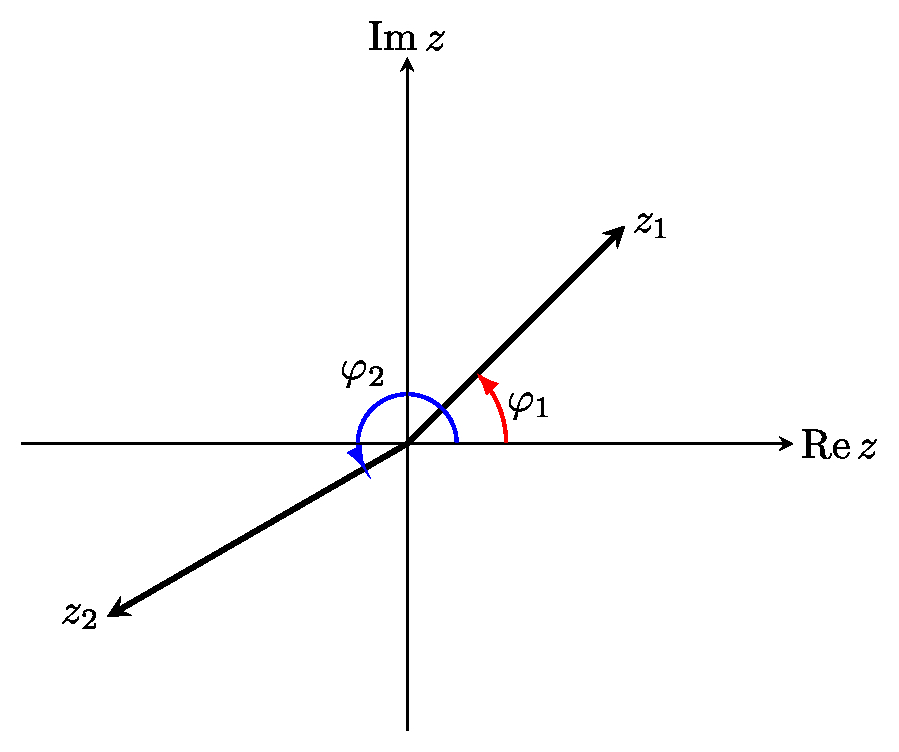
Отсюда можно вывести тригонометрическую запись $$ z = \rho(\cos\varphi + i\sin\varphi). $$ Строго говоря, аргумент комплексного числа определен не однозначно, в общем виде аргумент можно записать как \begin{equation*} \operatorname{Arg} z = \arg z + 2\pi k ,\text{ где } k\in\mathbb Z, \end{equation*} где $0\leq \arg z <2\pi$ - главное значение аргумента. В свою очередь, главное значение аргумента комплексного числа определено однозначно (и принимает значения в промежутке $[0,2\pi)$). Пусть $z_1=\rho_1(\cos\varphi_1+i\sin\varphi_1)$, а $z_2=\rho_2(\cos\varphi_2+i\sin\varphi_2)$ - два комплексных числа (в тригонометрической записи), тогда несложно проверить, что их произведение можно вычислить следующим образом: \begin{equation}\label{fr:trig-product} z_1\cdot z_2 = \rho_1\cdot\rho_2(\cos(\varphi_1+\varphi_2)+i\sin(\varphi_1+\varphi_2)). \end{equation} Другими словами, модуль произведения двух комплексных чисел равен произведению модулей этих чисел, сумма аргументов сомножителей является аргументом произведения.

Упражнение. Вывести формулу произведения \eqref{fr:trig-product}.

Для любого целого числа $k$ верно \begin{equation}\label{eq:pow_trig} z^k = \rho^k(\cos k\varphi+i\sin k\varphi). \end{equation} Другими словами, формула \eqref{eq:pow_trig} задаёт способ возведения комплексного числа в степень.\index{возведение в степень} При $\rho=1$ из выражения \eqref{eq:pow_trig} выводится формула Муавра: \begin{equation}\label{fr:muavr} (\cos\varphi+i\sin\varphi)^k = \cos k\varphi+i\sin k\varphi. \end{equation} Эту формулу можно использовать для нахождения синусов и косинусов кратных углов.

Бесконечно удалённая точка

Введём понятие расширенной комплексной плоскости, состоящей из обычной комплексной плоскости и единственного бесконечно удалённого элемента -бесконечно удалённой точки $z = \infty$. Отметим, что аргумент комплексного числа $\infty$ не определён, так же как и его действительная и мнимая часть. Для комплексного числа $\infty$ полагают следующие алгебраические свойства:

$\dfrac{1}{\infty}=0; \quad \dfrac{1}{0}=\infty$;
$z+\infty=\infty, z-\infty=\infty$;
$z\cdot\infty=\infty, \quad \text{при }z\ne0$;
$\dfrac{z}{\infty}=0,\quad\text{при } z\ne\infty, \quad \text{а операции }$ $\infty+\infty,\quad 0\cdot\infty,\quad \dfrac{\infty}{\infty} - \text{лишены смысла}$.

Отметим, что так как $\dfrac{0}{0}=0\cdot\dfrac{1}{0}=0\cdot\infty$, то операция $\dfrac{0}{0}$ также не определена.

Сфера Римана

Другим геометрическим представлением комплексных чисел является сфера Римана. Рассмотрим трехмерное евклидово пространство с координатами $(\xi,\eta,\theta)$ и совместим комплексную плоскость $\mathbb C$ с плоскостью $O\xi \eta$ так, чтобы действительная ось совпала с осью ${O\xi}, $ мнимая ось с осью $O{\eta},$ и положительные направления на соответствующих осях совпадали. Обозначим через $S$ сферу с центром в точке $\left(0,0,\frac{1}{2}\right)$ радиуса $\frac{1}{2}$, имеющую уравнение \begin{equation}\label{rim-sph} {\xi}^2+{\eta}^2+\left(\theta - \frac{1}{2}\right)^2 =\frac{1}{4}, \end{equation} а точку $(0,0,1)$ назовем \полюсом сферы $S$ и обозначим символом $P.$ Соединим отрезком точку $\mathbf{z}\in \mathbb C$ с полюсом $P$, при этом отрезок пересечет сферу $S$ в единственной точке $M(\xi,\eta,\theta)$. Точка $M$ называется стереографической проекцией точки $\mathbf{z}\in \mathbb C$ на сферу $S$.

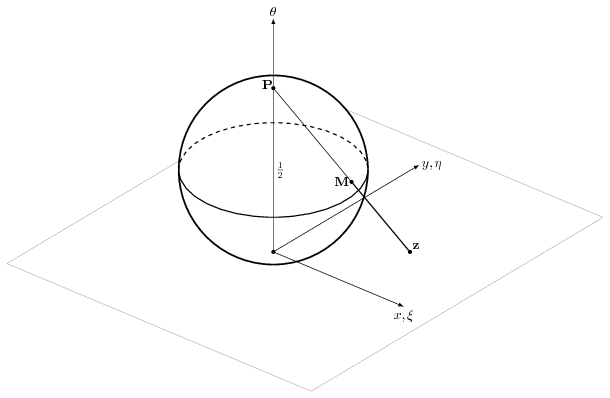
Стереографическая проекция устанавливает взаимно однозначное соответствие между точками комплексной плоскости $\mathbb C$ и точками сферы $S$ с выколотым полюсом $P$. В силу колинеарности точек $P(0,0,1)$, $M(\xi,\eta,\theta)$ и $\mathbf{z}(x,y,0)$ имеем $$\frac{\xi}{x} = \frac{\eta}{y} = \frac{1-\theta }{1},$$ откуда выводим \begin{equation}\label{sterion-coordinate} x= \frac{\xi}{1-\theta}, \ y= \frac{\eta}{1-\theta}, z= \frac{\xi + i\eta}{1-\theta}. \end{equation} Поскольку $$ |z|^2 = \frac{{\xi}^2 + {\eta}^2}{(1-\theta)^2}, $$ то из уравнения сферы \eqref{rim-sph} получаем \begin{equation}\label{sterion-z^2} |z|^2 = \frac{\theta}{1-\theta}. \end{equation} Выражая из равенства \eqref{sterion-z^2} значение $\theta$ и подставляя его в равенства \eqref{sterion-coordinate}, находим \begin{equation}\label{sterio-projection} \xi = \frac{x}{1+|z|^2}, \ \eta =\frac{y}{1+|z|^2}, \ \theta = \frac{|z|^2}{1+|z|^2}. \end{equation} Формулы \eqref{sterio-projection} называют формулами стереографической проекции. При неограниченном удалении точки $z$ от нуля в произвольном направлении (вдоль произвольной прямой) образ этой точки на сфере всегда будет стремиться к полюсу $P$. Если мы доопределим стереографическую проекцию, полагая полюс $P$ образом бесконечно удаленной точки, то получим взаимно однозначное соответствие между расширенной комплексной плоскостью $\overline{\mathbb C}$ и сферой $S$.

Упражнение. Доказать круговое свойство стереографической проекции: всякая окружность или прямая на комплексной плоскости $\mathbb C$ отображается стереографической проекцией в окружность на сфере $S$, и обратно, прообразом всякой окружности на сфере $S$ является либо окружность либо прямая на плоскости $\mathbb C$.

Упражнение. Доказать свойство консерватизма углов: угол между любыми гладкими кривыми на комплексной плоскости равен углу между образами этих кривых, лежащими на сфере $S$.

Кривые на комплексной плоскости

Пусть дана комплекснозначная функция $\gamma(t)$, непрерывная на отрезке $[a, b]$. Когда точка $t$ пробегает отрезок $[a, b]$, точка $\gamma(t) = x(t) + iy(t)$ пробегает некоторое множество в комплексной плоскости. Это множество вместе с указанием порядка, в котором проходятся все его точки, называется непрерывной кривой, а уравнение $z = \gamma(t)$ - параметрическим уравнением этой кривой. Порядок, в котором в котором проходятся точки называется ориентацией кривой.

Пример. Параметризация отрезка, соединяющего точки $z_1$ и $z_2$ имеет вид $$ \gamma(t) = z_1 + t\cdot(z_2-z_1), \qquad t\in[0,1]. $$ При этом кривая $\gamma$ ориентирована в направлении от $z_1$ к $z_2$.

Кривая, не имеющая самопересечений называется простой кривой или простым контуром.

Кривая называется замкнутой, если её начало совпадает с её концом, то есть если она имеет параметрическое уравнение \begin{equation*} z = z(t),\quad a\leq t\leq b, \quad \text{для которого} \quad z(a) = z(b). \end{equation*}

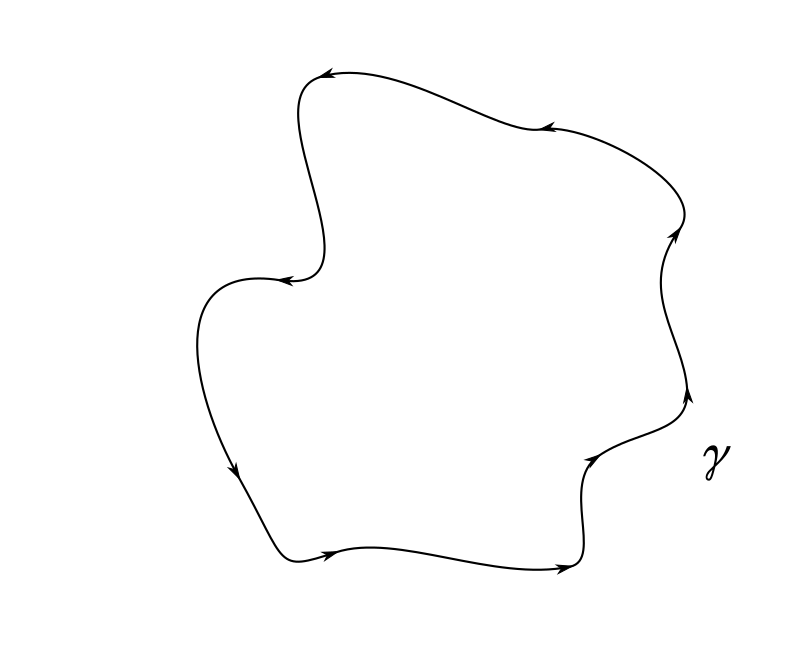
Замкнутая кривая без самопересечений, ориентированная против часовой стрелки

Пример. Одной из самых простых замкнутых кривых является окружность. Пусть $C(z_0,R)$ - окружность с центром в точке $z_0$ и радиусом $R$. Тогда параметризация этой окружности имеет вид $$ \gamma(t) = z_0 + Re^{it}, \qquad t\in[0,2\pi]. $$ При этом кривая $\gamma$ ориентирована против часовой стрелки. Если требуется ориентация по часовой стрелке, то следует выбрать уравнение вида $$ \gamma(t) = z_0 + Re^{-it}, \qquad t\in[0,2\pi]. $$ Также приведём параметризацию эллипса $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ $$ \gamma(t) = a\cos t + b\sin t, \qquad t\in[0,2\pi] $$ против часовой стрелки, и по часовой стрелке $$ \gamma(t) = a\cos t - b\sin t, \qquad t\in[0,2\pi]. $$

Если кривая $\gamma$ имеет хотя бы одно параметрическое уравнение $z = \gamma(t), \quad a\leq t\leq b$, с функцией $\gamma(t)$, имеющей на отрезке $[a, b]$ непрерывную и отличную от нуля производную, то $\gamma$ называется гладкой кривой.

Производная $\gamma'(t_0) = x'(t_0)+iy'(t_0)$ - является касательным вектором к кривой $\gamma$ в точке $\gamma(t_0)$. Непрерывная кривая $\gamma$ называется кусочно-гладкой кривой, если её можно разбить на конечное число частей, каждая из которых является гладкой кривой.

Топология комплексной плоскости

Приведём основные топологические понятия, которые потребуются в данном курсе. Пусть $z,w\in\mathbb C$, тогда $|z-w|$ - расстояние между точками $z$ и $w$. Расстояние от точки до множества и расстояние между множествами определяются следующим образом $$\operatorname{dist}(z, A) = \inf\limits_{w\in A}|z-w|, \quad \operatorname{dist}(A, B) = \inf\limits_{z\in A, w\in B}|z-w|.$$ Фиксируем комплексное число $a\in\mathbb C$ и вещественное число $r>0$, тогда числа $z$, удовлетворяющие равенству $|a-z|=r$, составляют множество точек, удалённых от $a$ на расстояние $r$. Другими словами, это окружность с центром в $a$ и радиусом $r$.

Множество точек $B(a,r) = \{z\in\mathbb C : |z-a| < r\}$ образуют круг.

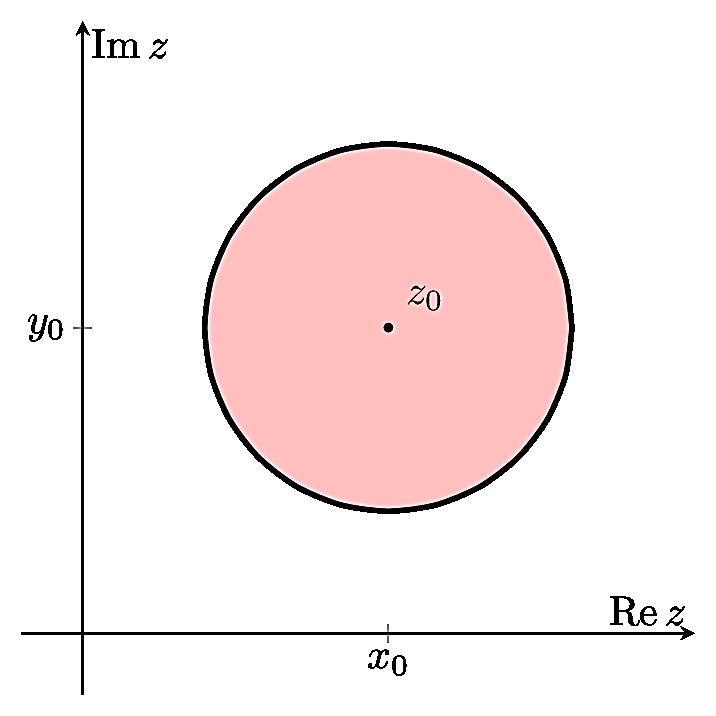
Также множество $B(a,r)$ называют окрестностью точки $a$ (или $r$-окрестностью). Однако $r$-окрестностью бесконечно удалённой точки называют множество $\overline{\mathbb C}\setminus \overline{B(a,r)}$, то есть внешность круга. Окрестностью бесконечно удалённой точки на сфере Римана является "шапочка", то есть часть сферы, расположенная выше некоторой плоскости $\theta=a$, \ $0< a < 1$.

Пусть $E\subset\mathbb C$.
1. Точка $a$ называется внутренней точкой множества $E$, если найдётся окрестность $B(a, r)\subset E$.
2. Точка $b$ называется textbf{граничной точкой множества $E$, если всякая окрестность $B(b, r)$ содержит точки из $E$ и из $\mathbb C\setminus E$.
3. Точка $c$ называется предельной точкой множества $E$, если всякая окрестность $B(c, r)$ содержит точки из $E$, отличные от $c$.
4. Точка $d$ называется изолированной точкой множества $E$, если $d\in E$ и найдётся окрестность $B(d, r)$, которая не содержит других точек из $E$.

Множество $E\subset\mathbb C$ называется открытым, если все его точки внутренние. Множество $E\subset\mathbb C$ называется замкнутым, если оно содержит все свои граничные точки.

Пример. Пусть $R>0$ и $z_0\in\mathbb C$, тогда множества $\{z\in\mathbb C : |z-z_0|R\}$ открыты, в то время как множество $\{z\in\mathbb C : |z-z_0|\leq R\}$ - замкнуто.

Пример. $\mathbb C$ и пустое множество $\emptyset$ - открытые множества (и в то же время замкнутые).

Множество всех граничных точек множества $E$ называется границей и обозначается $\partial E$. Множество всех внутренних точек множества $E$ называется внутренностью и обозначается $\operatorname{int} E$. Объединение множества и его границы $\partial E\cup E$ называется замыканием и обозначается $\overline{E}$.

Пример. Пусть $E = \{z\in\mathbb C : |z- z_0|< R \}$, тогда $\overline{E} = \{z\in\mathbb C : |z- z_0|\leq R \}$ и $\partial E = \{z\in\mathbb C : |z- z_0| = R \}$. $\overline{E}$ --- замкнутый диск, а $\partial E$ - окружность.

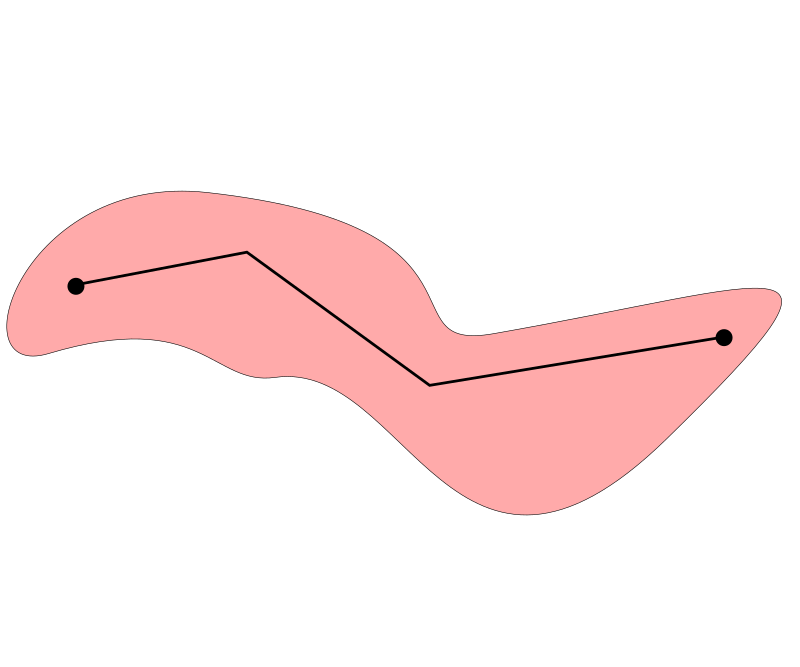
Множество $E$ называется связным, если не существует двух открытых множеств $U_1$ и $U_2,$ удовлетворяющих условиям $$E\subset U_1 \cup U_2, \ E\cap U_1 \ne \emptyset, \ E\cap U_2 \ne \emptyset, \ U_1\cap U_2 = \emptyset.$$ Это определение связности в случае непустого открытого множества $D$ равносильно тому, что любые две точки множества $D$ можно соединить ломаной, целиком лежащей в данном множестве.

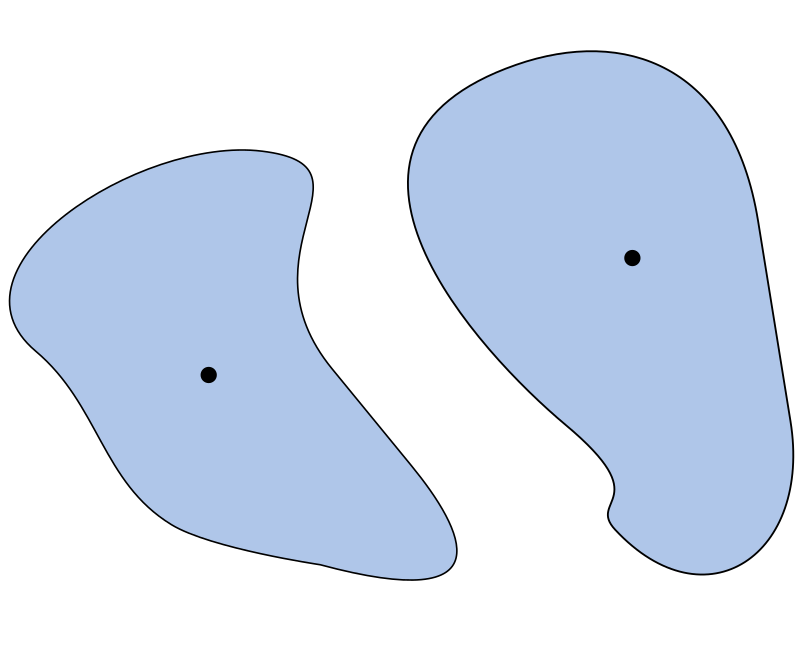
Область- это открытое связное множество.

Число компонент границы данной области называется\порядком связности этой области. Далее рассматриваются только области с конечным порядком связности, иными словами конечносвязные области.

Множество $E\subset\mathbb C$ называется ограниченным, если существует такой круг $B(0,R),\ R<\infty,$ что $E\subset B(0,R)$, то есть $|z|<R$ для любого $z\in E$.