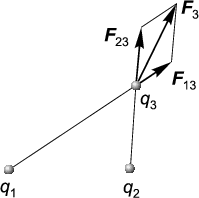
4 Принцип суперпозиции

§4 Принцип суперпозиции

Если E→1(r→) — поле системы зарядов №1, а E→2(r→) — поле системы зарядов №2, то при наличии зарядов обоих систем

E→(r→) = E→1(r→) + E→2(r→).

(4.1)

Рис. 1.3 поясняет сказанное.

Рис. 1.3:

Принцип суперпозиции. В отсутствие заряда q2 на пробный заряд q3 действует сила F→13 = q3E→1, а в отсутствие заряда q1 — сила F→23 = q3E→2. При наличии обоих зарядов действующая сила равна их сумме, F→3 = F→13 + F→23 = q3E→. Отсюда следует, что в месте нахождения пробного заряда E→ = E→1 + E→2.

Простейшая система состоит из одного заряда. Следовательно, электрическое поле системы зарядов равно сумме полей, создаваемых каждым зарядом в отдельности, в отсутствие других зарядов:

E→(r→) = ∑ j qj ∣r→ −r→j∣2 r→ −r→j ∣r→ −r→j∣ .

(4.2)

Здесь qj,r→j — заряд и радиус-вектор j-го заряда. Правило сложения (4.1) называют принципом суперпозиции, а формула (4.2) является следствием принципа суперпозиции и закона Кулона.

Принцип суперпозиции является экспериментальным фактом. В электродинамике он рассматривается как абсолютно точный в том смысле, что никакие отклонения от него не обнаружены. Принцип суперпозиции для электрического поля не столь очевиден, как могло бы показаться на первый взгляд. Например, можно предположить, что он нарушается в очень сильном поле аналогично тому, как в твердом теле упругие напряжения можно складывать только при условии, что они достаточно малы (при больших деформациях тело разрушается). Однако эксперименты свидетельствуют, что даже на поверхности тяжёлых ядер, где электрическое поле достигает громадных значений, принцип суперпозиции выполняется. Другое дело, что при полях, примерно в 100 раз меньших, проявляются эффекты поляризации вакуума в результате рождения электрон-позитронных пар. Это приводит к квантово-механической нелинейности взаимодействия зарядов.

▸Задача 4.1

Верно ли утверждение, что сила взаимодействия двух точечных зарядов не изменяется в присутствии других зарядов?

▸Задача 4.2

Верно ли утверждение, что сила взаимодействия двух заряженных тел не изменяется в присутствии других заряженных тел?

▸Задача 4.3

Можно ли измерить силу взаимодействия двух точеных зарядов в системе трёх зарядов, не удаляя третий заряд?

[next] [prev] [prev-tail] [front] [up]