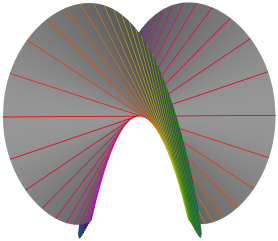
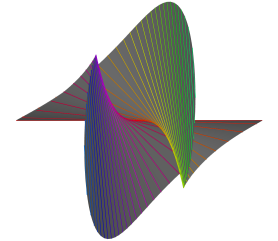
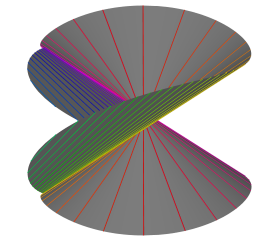
Наиболее широко известен изучаемый в школе дискриминант квадратного уравнения. Аналогично ему, дискриминант $\Delta$ кубического уравнения $t^3 + xt^2 + yt + z = 0$ с неизвестной $t$ -- это полином степени 4 от коэффициентов уравнения, здесь $x$, $y$, $z$, принимающий значение 0 тогда и только тогда, когда уравнение имеет кратные корни. Условие $\Delta = 0$ определяет в пространстве с декартовыми координатами $(x,y,z)$ поверхность с достаточно интересной геометрией. Она содержит линию из особых точек -- ребро возврата, являющееся скрученной кубической параболой, и заметается касательными к ней прямыми. Ребро возврата соответствует кубическим уравнениям с корнем кратности 3.

Вот этот дискриминант под трёмя разными углами зрения (в шаре радиуса 18 с центром в начале координат). Нажмите на картинки для перехода к 3д.

Отдельно проиллюстрировано применение этого дискриминанта в дифференциальных уравнениях.