Линейные автономные системы третьего порядка
Для однородной линейной системы обыкновенных дифференциальных уравнений
с постоянными коэффициентами
и характеристическим полиномом $t^3 + xt^2 + yt + z$,
в пространстве параметров $(x,y,z)$
нарисована схема типов поведения траекторий.
Схема представлена в шаре радиуса 18 с центром в начале координат.
Нажмите на картинки для перехода к 3д.
Пояснения ниже.
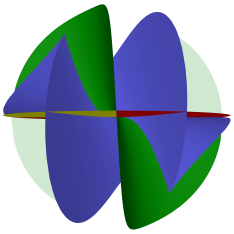
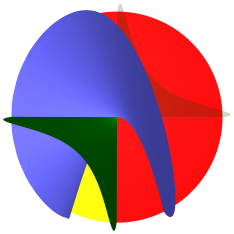
Границами зон основных типов являются следующие поверхности:
-
Красная и жёлтая плоскость $z=0$.
На ней расположены характеристические полиномы вырожденных матриц.
-
Зелёный гиперболический параболоид $xy-z=0$.
На его тёмной половине $y>0$ расположены полиномы,
имеющие пары чисто мнимых корней.
Полупрозрачная вторая половина параболоида не играет никакой особой роли.
-
Синяя поверхность (алгебраическая степени 4) это
дискриминант кубического уравнения
$t^3 + xt^2 + yt + z = 0$.
На ней по определению расположены полиномы, имеющие кратные корни.
Эта поверхность имеет ребро возврата;
на нём расположены полиномы, имеющие корень кратности 3.
Согласно критерию Рауса -- Гурвица,
устойчивы в точности системы, попадающие в зону $x>0$, $xy>z>0$
между жёлтой четвертью плоскости
и возвышающейся над ней четвертью зелёного параболоида.
Иными словами, у всех таких систем точка покоя в начале координат является стоком.
Между плоскостью и ребром возврата дискриминанта лежит остроугольная подзона систем
с тремя отрицательными вещественными собственными числами (аналоги узлов),
а остальная часть зоны стоков занята аналогами фокусов.
Симметрично зоне стоков,
между частью красной плоскости и тёмной частью параболоида
расположена зона источников,
таким же образом разделённая синим дискриминантом
на подзоны с аналогами узлов и фокусов.
Большую часть пространства параметров занимают аналоги сёдел
в том смысле,
что такие точки имеют как входящие траектории, так и выходящие.
Они делятся на 4 основных типа
соответственно поведению входящих и выходящих траекторий:
- плоскость входящих как фокус и прямая выходящих;
- плоскость входящих как узел и прямая выходящих;
- прямая входящих и плоскость выходящих как узел;
- прямая входящих и плоскость выходящих как фокус.
Границей между вторым и третьим типами служит красная плоскость.
Границей между остальными типами опять служит синий дискриминант.
Приближаясь к зелёному параболоиду с любой стороны,
фокусы в пределе переходят в центры.
Приближаясь к синему дискриминанту,
фокусы и узлы в пределе переходят в вырожденные и дикритические узлы.



