7 Электрический потенциал

§7 Электрический потенциал

Электростатическое поле, т.е. электрическое поле неподвижных зарядов, потенциально. Это означает, что работа электрического поля по перемещению пробного заряда по любому замкнутому контуру равна нулю:

A = −q ∮ E→dr→ = 0.

(7.1)

Потенциальность электростатического поля есть следствие закона сохранения энергии, ибо в противном случае можно было бы построить вечный двигатель 1-го рода.

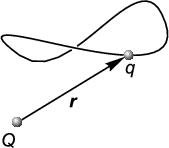
Рис. 1.13:
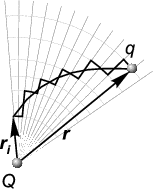
Доказательство равенства (7.1) очень просто. Вследствие принципа суперпозиции достаточно проверить, что равна нулю работа по замкнутому контуру в поле точечного заряда (рис. 1.13). Вычислим интеграл

A = - \int r \to i r \to q Q r \to d r \to r 3 .

соответствующий работе по перемещению пробного заряда q в электрическом поле E→ = Qr→∕r3 заряда Q из начальной точки с радиус вектором r→i в наблюдения точку с радиус-вектором r→ по произвольному контуру. Дифференцируя тождество r→2 = r2, легко убедиться, что r→dr→ = rdr. Поэтому криволинейный интеграл сводится к определённому между радиусами ri и r начальной точки и точки наблюдения:

A = - \int r i r q Q d r r 2 = q Q r - q Q r i .

Отсюда следует, что при любом выборе этих точек работа определяется только их положением и не зависит от формы пути. На замкнутом пути конечная точка совпадает с начальной, т.е. r = ri, поэтому A = 0.

Приведенное доказательство можно пояснить следующими рассуждениями. Любой контур можно представить в виде сегментов достаточно малого размера, поочередно идущих то по радиальному направлению от заряда Q, то по сферической поверхности, как показано на рис. 1.14.

Рис. 1.14:

Траектория перемещения пробного заряда и её приближение отрезками радиальных линий и дугами окружностей

Перемещение пробного заряда q по сфере перпендикулярно кулоновской силе, поэтому электрическое поле там не совершает работу. Все такие перемещения можно просто исключить. Тогда произвольный контур сжимается в отрезок прямой линии, идущей по радиусу от источника поля Q. Пробный заряд проходит этот отрезок дважды: сначала в одну сторону, потом обратно. На каждом участке обратного пути на него действует та же сила, что и при движении вперед, но так как заряд движется в противоположном направлении, работа имеет противоположный знак. Таким образом, при возвращении в точку старта работа электрического поля обращается в нуль.

Рис. 1.15:

Работа A132 по перемещению заряда в электростатическом поле из точки 1 в точку 2 по пути 132 равна работе A142 по перемещению того же заряда по пути 142. При перемещении заряда по замкнутому пути 13241 работа на участке 241 изменит знак: A241 = −A142. Поэтому A13241 = A132 + A241 = 0.

В потенциальном электрическом поле работа не зависит от формы пути. Это утверждение можно рассматривать в качестве альтернативного определения свойства потенциальности электрического поля. Два определения полностью эквиваленты, как должно быть ясно из приведенных выше рассуждений. Формальное же доказательство состоит в том, что если замкнутый контур разбить на две траектории, имеющие общие точки старта и финиша, то из равенства работы при перемещении пробного заряда по этим траекториям следует равенство нулю полной работы по замкнутому контуру (рис.1.15). И наоборот, из равенства нулю работы по замкнутому контуру следует равенство работы при перемещении пробного заряда по любым траекториям с общими точками старта и финиша.

Зафиксируем точку старта r→i, считая, что траектория перемещения заряда может финишировать в точке наблюдения с произвольными координатами r→ = (x,y,z) (рис. 1.14). Тогда интеграл

ϕ(r→) = −∫ r→ir→E→⋅dr→

(7.2)

является однозначной функцией координат точки наблюдения, поскольку форма траектории не влияет на её значение. Функцию ϕ называют скалярным потенциалом электрического поля; используют также термины электростатический или электрический потенциал. Скалярный потенциал равен работе, совершаемой электрическим полем при перемещении единичного пробного заряда из точки наблюдения в ту точку, где потенциал условно принят равным нулю. Если нуль потенциала не задан, то говорят, что потенциал определен с точностью до аддитивной константы.

Пробный заряд q в электростатическом поле обладает потенциальной энергией

U(r→) = q ϕ(r→).

(7.3)

Потенциальная энергия также определена с точностью до константы. Имеет смысл только разность потенциальной энергии U(r→) − U(r→i) между двумя точками. Эта разность равна работе по перемещению заряда из точки r→i в точку r→:

A = U(r→) − U(r→i).

(7.4)

Потенциал точечного заряда Q нетрудно найти, повторив вычисления начала параграфа:

ϕ (r \to) = - \int r i r Q d r r 2 = Q r - Q r i .

Приняв за точку нуля бесконечно удаленную точку ri = ∞, получим

ϕ = Q r .

(7.5)

Если заряд qj находится в произвольной точке с радиус-вектором r→j, то

ϕ (r \to) = q j ∣ r \to - r \to j ∣ .

Потенциал системы зарядов есть сумма потенциалов отдельных зарядов:

ϕ(r→) = ∑ j q ∣r→ −r→j∣ .

(7.6)

Это следует из принципа суперпозиции.

В системе СИ потенциал измеряется в вольтах (В). В абсолютной гауссовой системе единицей измерения является статвольт (стВ):

[ϕ] = 1стВ ≈ 300В .

(7.7)

При перемещении заряда 1Кл между точками с разностью потенциала 1В совершается работа 1Дж, т.е. 1В = 1Дж∕Кл. Электрическое поле измеряется соответственно в вольтах на метр (В/м) и в статвольтах на сантиметр (стВ/см):

[E] = 1стВ/см ≈ 3⋅104 В/м .

(7.8)

▸Задача 7.1

Оценить напряженность электрического поля на поверхности тяжёлых ядер.

▸Задача 7.2

Найти потенциал однородного поля.

Решение: Приняв за нуль потенциала начало координат, из (7.2) получаем:

ϕ (r \to) = - E \to \cdot r \to,

где E→ — постоянный вектор напряженности электрического поля. В декартовых координатах это выражение принимает вид

ϕ (x, y, z) = - (E x x + E y y + E z z) .

В сферических координатах это же выражение переходит в

ϕ (r, θ) = - E r cos θ,

если широтный угол θ отсчитывать от направления E→. ▸Задача 7.3

Вычислить электрический потенциал шара, равномерно, заряженного по объёму или поверхности.

▸Задача 7.4

Вычислить электрический потенциал бесконечной прямой нити и бесконечно длинного равномерно заряженного цилиндра.

ДОПОЛНИТЕЛЬНО

Из жизни великих людей: А.Вольта (Классики, стр. 227)

[next] [prev] [prev-tail] [front] [up]