Задача №597 |
| Слой внутри цилиндрического конденсатора содержит
непроводящий диэлектрик углового размера α с диэлектрической проницаемостью ε и, в остальной области, проводник с проводимостью σ (диэлектрическая проницаемость равна 1) (см. рисунок). Найти время релаксации зарядов, нанесенных на пластины конденсатора. |

|
|
|
Показать решение
|
|
Задача №596 |
| Слой внутри плоского конденсатора содержит непроводящий диэлектрик площадью S1 с диэлектрической проницаемостью ε и проводник площадью S2 с
проводимостью σ (ε2=1) (см. рисунок). Найти время релаксации зарядов, нанесенных на пластины конденсатора. |

|
|
|
Показать решение
|
|
Задача №595 |
| В одну половину цилиндрического конденсатора с длиной L и радиусами обкладок R1 и
R2≪L вставлен без зазоров цилиндрический
слой с диэлектрической проницаемостью ε1, а в
другую половину – с диэлектрической проницаемостью ε2. Конденсатор зарядили до напряжения U0, после чего внешний
источник отключили. Найти работу, которую нужно совершить, чтобы вынуть
диэлектрический слой с ε1 (сила трения отсутствует). |

|
|
|
Показать решение
|
|
Задача №594 |
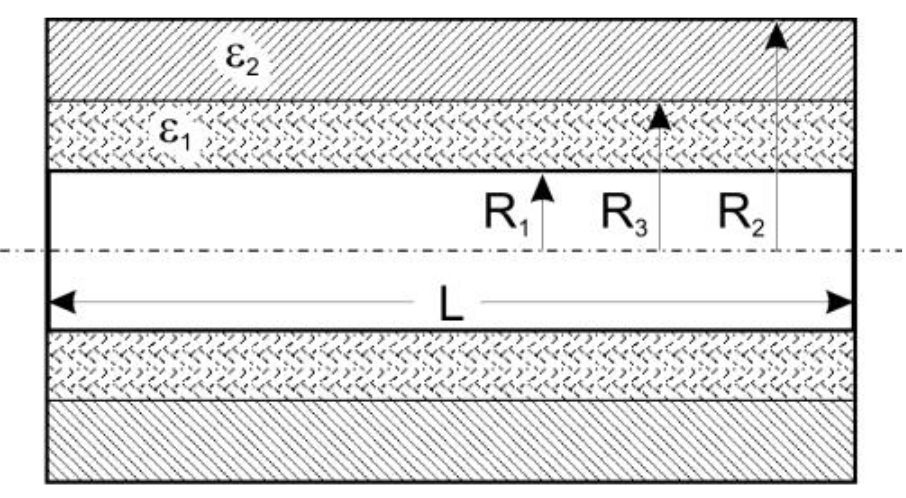
| В цилиндрический конденсатор с длиной L
и радиусами обкладок R1 и R2≪L вставлены
без зазоров два коаксиальных цилиндрических
слоя с диэлектрическими проницаемостями ε1
и ε2. Радиус границы между слоями R3. Конденсатор зарядили до напряжения U0, после чего источник отключили. Найти работу, которую нужно совершить, чтобы вынуть внешний диэлектрический слой (сила трения отсутствует). |
|
|
|
Показать решение
|
|
Задача №592 |
| Пространство между двумя круглыми параллельными проводящими
пластинами радиуса a, расположенными на расстоянии d(d≪a), заполнено средой, диэлектрическая проницаемость которой меняется по закону ε(r)=ε0cosπr26a2, где r – расстояние от оси, проходящей через центры пластин. Найти емкость. |

|
|
|
Показать решение
|
|
Задача №559 |
| Найти изменение ёмкости плоского конденсатора δC при внесении в него
маленького диэлектрического шарика с проницаемостью ε. Радиус шарика a
мал по сравнению с расстоянием от его центра до пластин конденсатора, расстояние между которыми d.
Краевыми эффектами пренебречь, до внесения шарика конденсатор был пуст. |

|
|
|
Показать решение
|
|
Задача №549 |
| Верхнее полупространство (z>0) пусто, а нижнее заполнено
диэлектриком с диэлектрической проницаемостью ε. Над диэлектриком на одинаковом расстоянии a от его плоской границы и на расстоянии l друг от друга расположены точечные заряды q1 и q2. Найти проекции силы, действующей на заряд q2, на вертикальное (Fz) и горизонтальное (Fx) направления. |

|
|
|
Показать решение
|
|
Задача №548 |
| Верхнее полупространство (z>0) пусто, а нижнее заполнено
диэлектриком с диэлектрической проницаемостью ε. Внутри диэлектрика на одинаковом расстоянии a от его плоской границы и на расстоянии l друг от друга расположены точечные заряды q1
и q2. Найти проекции силы →F, действующей на заряд q2, на вертикальное (Fz) и горизонтальное (Fx) направления. |

|
|
|
Показать решение
|
|
Задача №546 |
| Пространство между двумя плоскими проводящими
пластинами площадью S, расположенными параллельно
друг другу на расстоянии d(d≪√S), заполнено средой,
диэлектрическая проницаемость которой меняется по
ε(z)=ε0cosπz2d, где z отсчитывается от середины конденсатора в направлении,
перпендикулярном пластинам. Найти ёмкость конденсатора. |

|
|
|
Показать решение
|
|
Задача №521 |
| Цилиндрический конденсатор с обкладками радиуса a и b заполнен диэлектриком, проницаемость
которого меняется по закону ε(α)=ε0(1+sin2α).
Найти емкость на единицу длины конденсатора. |
|
|
|
Показать решение
|
|
Задача №520 |
| Сферический конденсатор с обкладками радиуса a и b заполнен диэлектриком, проницаемость
которого меняется по закону ε(θ)=ε0(1+sin2θ).
Найти емкость конденсатора. |
|
|
|
Показать решение
|
|
Задача №502 |
| Металлический шар радиуса a помещен на плоскую границу раздела двух диэлектриков с диэлектрическими проницаемостями ε1 (верхнее полупространство) и ε1 (нижнее полупространство) так, что центр шара совпадает с границей раздела диэлектриков z=0 и находится в точке начала координат (x=0,y=0). Система помещена во внешнее поле, направленное нормально к границе раздела, так, что электрическое поле вдали от шара и границы раздела однородно, а его напряженность в диэлектрике ε1 равна E1. Определить напряженность электрического поля и его индукцию во всем пространстве. |

|
|
|
Показать решение
|
|
Задача №492 |
| Четыре электрода расположены на горизонтальной границе проводящего полупространства с удельной проводимостью σ и диэлектрической проницаемостью ε. В точках А и В подключён источник тока, а в точках М и N измеряется напряжение. Найти «кажущееся» сопротивление R∗=UMN/IAB,
если AM=MN=NB=l и лежат на одной прямой (схема Веннера, левый рис.). Что будет, если проводящее полупространство разделено вертикальной границей на две области с удельной проводимостью σ1 и σ2, диэлектрической проницаемостью ε1 и ε2 так, что электроды расположены вдоль границы раздела (правый рис)? Проверить ответ при σ1=σ2=σ. |

|
|
|
Показать решение
|
|
Задача №491 |
| К плоской горизонтальной границе диэлектрика с проницаемостью ε, занимающего верхнее полупространство, поднесли проводящую пластину площадью S
и массой m. Какой минимальный заряд следует сообщить пластине, чтобы она не упала? Ускорение свободного падения g. |

|
|
|
Показать решение
|
|
Задача №490 |
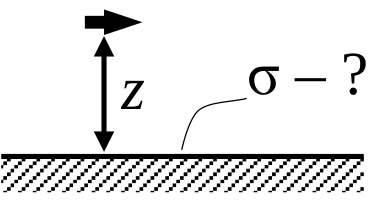
| Точечный диполь →d закреплён на расстоянии h от плоской границы проводника. Найти распределение поверхностной плотности σ индуцированного заряда на границе, если →d параллелен границе. |
|
|
|
Показать решение
|
|
Задача №485 |
| Точечный заряд q расположен внутри сферической полости в
незаряженном проводящем шаре радиуса a. Найти плотность зарядов на внешней поверхности шара. |

|
|
|
Показать решение
|
|
Задача №484 |
| Бесконечно длинная тонкая нить, равномерно заряженная с линейной плотностью ϰ, протянута внутри цилиндрической полости
в незаряженном проводящем бесконечно длинном цилиндре радиуса a. Оси нити, полости и цилиндра параллельны. Найти
плотность зарядов на внешней поверхности цилиндра. |

|
|
|
Показать решение
|
|
Задача №465 |
| На некотором расстоянии от плоской границы раздела двух диэлектриков с диэлектрическими
проницаемостями ε1 и ε2 находится точечный заряд q (в среде
с проницаемостью ε1). Найти поток Φ напряженности
электрического поля →E через область границы (включая границу), имеющую форму круга с осью,
проходящей через источник, и угловой радиус, видимый из источника, равный θ. |

|
|
|
Показать решение
|
|
Задача №457 |
| Двугранный угол образован проводящими плоскостями y=0,x>0 и x=0,y>0. Плоскости электрически изолированы вдоль
соединяющего ребра, а между ними приложена разность потенциалов U.
Внешняя часть двугранного угла заполнена средой
с диэлектрической проницаемостью ε. Найти поверхностную
плотность свободного заряда σ(x)(x>0) в плоскости y=0. |

|
|
|
Показать решение
|
|
Задача №456 |
| Двугранный угол образован проводящими плоскостями y=0,x>0 и x=0,y>0.
Плоскости электрически изолированы вдоль
соединяющего ребра, а между ними приложена разность потенциалов U.
Внутренняя часть двугранного угла заполнена средой
с диэлектрической проницаемостью ε. Найти поверхностную
плотность свободного заряда σ(x)(x>0) в плоскости y=0. |

|
|
|
Показать решение
|
|
Задача №421 |
| Найти плотность заряда ρ(z) в плоском конденсаторе с квадратными электродами размером a×a, расстоянием
между пластинами d≪a, (см. рис.), разностью потенциала между пластинами U.
Удельная проводимость материала между пластинами зависит от z как σ(z)=σ0e−αz. |

|
|
|
Показать решение
|
|
Задача №416 |
| Определить емкость сферического конденсатора,
радиусы обкладок которого равны a и b, соответственно (a<b),
а диэлектрическая проницаемость диэлектрика между ними зависит от расстояния до центра как
ε(r)=b2r2tgra. |
|
|
|
Показать решение
|
|
Задача №415 |
| Определить емкость на единицу длины (погонную емкость) цилиндрического конденсатора,
радиусы обкладок которого равны a и b, соответственно (a<b),
а диэлектрическая проницаемость диэлектрика между ними зависит от расстояния до оси как
ε(r)=brtgra. |
|
|
|
Показать решение
|
|
Задача №372 |
Внутрь исходно незаряженного короткозамкнутого плоского конденсатора вставили электрет-брусок,
состоящий из частиц с дипольными моментами →d0,
ориентированными одинаково и ортогонально пластинам конденсатора; площадь пластин S,
а расстояние между ними h≪√S. Число частиц в единице объема n0.
Размеры электрета совпадают с размерами конденсатора.
Какой заряд протечет через проводник? Какую работу необходимо совершить, чтобы вставить электрет-брусок в конденсатор?
Указание. Считать, что потери энергии на излучении пренебрежимо малы. |
|
|
|
Показать решение
|
|
Задача №371 |
Внутрь плоского конденсатора вставили электрет-брусок, состоящий из частиц с дипольными моментами →d0,
ориентированными одинаково и ортогонально пластинам конденсатора; площадь пластин S, а расстояние между ними h≪√S. Число частиц в единице объема n0. Размеры электрета совпадают с размерами конденсатора. Пластины конденсатора замыкают проводником. Какой заряд протечет через проводник? (2 б.) Какое количество тепла выделится в проводнике? (+2 б.)
Указание. Считать, что потери энергии на излучении пренебрежимо малы. |
|
|
|
Показать решение
|
|
Задача №317 |
| Тонкостенный замкнутый прямоугольный сосуд наполовину заполнен жидким диэлектриком. На две противоположные
(наибольшие по площади) грани напылены металлические электроды, и к ним подключен измеритель емкости. В двух положениях, показанных на рисунке, проводятся измерения емкости. Отношения показаний равно CI/CII=9/8. Найдите диэлектрическую проницаемость ε жидкости. Поперечные размеры двух металлизированных граней много больше расстояния между ними. |

|
|
|
Показать решение
|
|
Задача №316 |
| Тонкостенный замкнутый прямоугольный сосуд наполовину заполнен жидким диэлектриком. На две противоположные
(наибольшие по площади) грани напылены металлические электроды, и к ним подключен измеритель емкости. В двух положениях, показанных на рисунке, проводятся измерения емкости. Отношения показаний равно CI/CII=4/3. Найдите диэлектрическую проницаемость ε жидкости. Поперечные размеры двух металлизированных граней много больше расстояния между ними. |

|
|
|
Показать решение
|
|
Задача №268 |
| В пространство с однородным электрическим полем E0
поместили диэлектрический цилиндр длиной l и сечением S (l≪S)
с диэлектрической проницаемостью ε.
Ось цилиндра и направление электрического поля E0 совпадают. Оценить электрическое поле,
создаваемое цилиндром на расстояниях r≫l. |
|
|
|
Показать решение
|
|
Задача №267 |
| В пространство с однородным электрическим полем E0
поместили диэлектрический цилиндр длиной l и сечением S (l≪S)
с диэлектрической проницаемостью ε.
Ось цилиндра и направление электрического поля E0 совпадают. Оценить вклад в электрическое поле от
цилиндра в его центре, в точке, находящейся посередине между его торцами. |
|
|
|
Показать решение
|
|
Задача №261 |
| В центр бесконечного диэлектрического цилиндра радиуса R с диэлектрической проницаемостью
ε поместили бесконечную однородно заряженную нить с линейной плотностью заряда ϰ. Найти
электрическое поле во всем пространстве и связанный заряд на единицу длины на границе цилиндра. |
|
|
|
Показать решение
|
|
Задача №260 |
| В центр диэлектрического шара радиуса R с диэлектрической проницаемостью ε поместили
точечный заряд q. Найти электрическое поле во всем пространстве и связанный заряд на границе шара. |
|
|
|
Показать решение
|
|
Задача №220 |
| Проводник A находится внутри замкнутой проводящей оболочки B.
Прослойка такого конденсатора состоит из двух областей c
границей раздела, образующей замкнутую поверхность (показана на рисунке пунктиром). Форма электродов и границы раздела произвольные.
Диэлектрическая проницаемость и проводимость областей равны ε1,σ1 и
ε2,σ2 соответственно. К электродам подано напряжение, такое, что от A к B
течет постоянный ток I. Какой свободный заряд Q накапливается при этом на границе раздела? |

|
|
|
Показать решение
|
|
Задача №217 |
| Оценить диэлектрическую проницаемость кристалла, имеющего структуру простой кубической решетки, в узлах которой находятся металлические шарики диаметром d≪a, где a – постоянная решетки. |
|
|
|
Показать решение
|
|
Задача №216 |
| Пространство с x<0,y<0,z<0 заполнено диэлектриком с диэлектрической проницаемостью ε1.
Остальное пространство заполнено диэлектриком с диэлектрической проницаемостью ε2.
В начало координат поместили точечный заряд q. Найти потенциал и напряженность электрического поля
во всем пространстве. |
|
|
|
Показать решение
|
|
Задача №210 |
| В вершине бесконечного конуса с углом раствора 2θ0 расположен заряд q.
Внутренняя часть конуса заполнена диэлектриком с диэлектрической проницаемостью
ε1, остальная часть пространства заполнена диэлектриком с
проницаемостью ε2. Найти потенциал и электрическое поле во всем пространстве. |

|
|
|
Показать решение
|
|
Задача №180 |
| Точечный заряд q помещен на плоскую границу полупространств с диэлектрической
проницаемостью ε1 и ε1 и проводимостью σ1 и σ2 соответственно.
Пренебрегая влиянием магнитного поля, найти зависимость заряда от времени q(t), если q(0)=q0. |

|
|
|
Показать решение
|
|
Задача №158 |
| Прямой полубесконечный провод с током I входит по нормали в проводящее полупространство z>0, в котором
σ=const, μ=1. Найти распределения потенциала φ(r,θ) и
объемной плотности тока →j(r,θ) в данном полупространстве (2 б); магнитное поле
→B во всем пространстве. (2 б) |

|
|
|
Показать решение
|
|
Задача №151 |
| Найти емкость сферического конденсатора, радиусы внутренней и внешней
обкладок a и b. Конденсатор заполнен диэлектриками с диэлектрическими
проницаемостями ε1 и ε2, как показано на рисунке. |

|
|
|
Показать решение
|
|
Задача №150 |
| Незаряженный диэлектрический шар радиуса b, содержащий
внутри себя проводящий шар радиуса a<b, находится в однородном
внешнем электрическом поле →E0. Найти распределение потенциала во
внешнем пространстве r>b, в диэлектрическом слое a<r<b и в металлическом шаре. |

|
|
|
Показать решение
|
|
Задача №136 |
| В среде с однородной проводимостью σ и диэлектрической проницаемостью ε(x),
распределенной, как показано на рисунке, течет постоянный ток с плотностью →j=j0→ex.
Найти плотность свободных и связанных зарядов во всем пространстве. |

|
|
|
Показать решение
|
|
Задача №130 |
| В плоскости z=0, разделяющей два полупространства, заполненных диэлектриками
с ε1(z<0) и ε2(z>0), расположены точечные заряды
в вершинах равнобедренного прямоугольного треугольника, как показано на
рисунке. Найти дипольный член в разложении потенциала φ1,2(x,y,z) для
обеих областей на расстояниях, много больших, чем a. |

|
|
|
Показать решение
|
|
Задача №129 |
| В плоскости z=0, разделяющей два полупространства, заполненных диэлектриками
с ε1(z<0) и ε2(z>0), расположены точечные заряды
в вершинах равнобедренного прямоугольного треугольника, как показано на
рисунке. Найти дипольный член в разложении потенциала φ1,2(x,y,z) для
обеих областей на расстояниях, много больших, чем a. |

|
|
|
Показать решение
|
|
Задача №126 |
| Сфера радиуса R заполнена диэлектриком проницаемостью ε. Потенциал на поверхности сферы
задан: φ(R,θ)=φ0sin2(θ/2). Зарядов внутри и вне сферы нет
(заряды, создающие потенциал, расположены только на поверхности диэлектрика). Найти потенциал и электрическое поле во всем пространстве, а также поверхностную плотность связанного заряда на границе диэлектрика. |
|
|
|
Показать решение
|
|
Задача №37 |
| Металлическая тонкостенная труба квадратного поперечного сечения заполнена однородными диэлектриками
ε1 и ε2, как показано на рисунке.
В области диэлектрика ε1 распределение потенциала известно: φ1(x,y)=φ0(a−x)ya2,
φ0=const. Найти распределение потенциала φ2(x,y) (2 б) и распределение свободных зарядов
на границе раздела диэлектриков (3 б). |

|
|
|
Показать решение
|
|
Задача №33 |
| Проводящая незаряженная сфера радиуса R и массой M свободно плавает в диэлектрике с проницаемостью ε,
погрузившись в нее на четверть своего объема. Какой заряд Q нужно нанести на сферу, чтобы она погрузилась на половину
своего объема? Ускорение свободного падения равно g. |
|
|
|
Показать решение
|
|
Задача №32 |
Слой проводника, бесконечно протяженный по координатам y и z, имеет проводимость, меняющуюся по закону:
σ(z)=σ01+psin(kz),где σ0, p<1, k – константы.
По слою бежит ток с объемной плотностью jz=j0=const.
Определить:
1) распределение потенциала внутри слоя (2 б);
2) потенциал в окружающем пустом пространстве (2 б);
3) распределение зарядов Σ(z) на поверхности слоя x=0 (2 б). |

|
|
|
Показать решение
|
|
Задача №31 |
Длинная металлическая труба квадратного поперечного сечения со сторонами a заполнена однородными диэлектриками
ε1 и ε2, как показано на рисунке. Граница раздела диэлектриков содержит равномерно распределенный
свободный заряд с поверхностной плотностью Σ0. Определить распределение потенциала в областях 1 и 2.
Указание: потенциал в области 1 искать в виде ϕ1=C1x(y−a), C1=const; аналогично в области 2. |

|
|
|
Показать решение
|
|
Задача №30 |
| Найти время релаксации заряда, помещенного на внутренний электрод сферического конденсатора, часть которого в секторе
с телесным углом Ω заполнена диэлектриком с проницаемостью ε, а оставшаяся часть
— проводником с проводимостью σ. |

|
|
|
Показать решение
|
|
Задача №20 |
| Диэлектрическая проницаемость среды в пространстве между обкладками плоского конденсатора задана функцией
ε={ε0(1+αx)при0<x<d/21приd/2⩽x⩽d,
где d – расстояние между обкладками. Найти напряженность поля E(x) между
обкладками, если приложенное напряжение равно U |
|
|
|
Показать решение
|
|
Задача №13 |
| В плоской границе раздела двух полупространств с диэлектрическими проницаемостями ε1 и ε2
находится равномерно заряженное кольцо радиуса a с общим зарядом q. Найти два первых ненулевых члена разложения
потенциала φ(r,θ) для расстояний r≫a |

|
|
|
Показать решение
|
|
Задача №11 |
| Найти емкость длинного (l≫b,a) цилиндрического конденсатора (сечение показано на рисунке),
верхняя и нижняя половины которого заполнены диэлектриком с проницаемостью
ε1, ε2 соответственно. Найти силу, действующую на внутреннюю обкладку,
если разность потенциалов между обкладками равна U. |

|
|
|
Показать решение
|
|
Задача №9 |
| Длинный цилиндрический конденсатор (радиусы обкладок a и c, длина L) имеет заполнение в виде двух концентрических слоев с различными
проводимостями (σ1 и σ2) и диэлектрическими проницаемостями (ε1 и ε2),
причем σ1/ε1=σ2/ε2. Радиус границы раздела слоев – b.
Внутренняя обкладка конденсатора заземлена, к внешней приложено постоянное напряжение U.
В некоторый момент времени t=t0 внешнюю обкладку мгновенно отключают от источника напряжения и соединяют с землей
через сопротивление R. Найти ток через сопротивление IR(t) |

|
|
|
Показать решение
|
|