Электрический диполь во внешнем электрическом поле. Сила и момент сил на электрический диполь во внешнем электрическом поле

Краткая теория

Сила на электрический диполь с моментом $\vec{d}$ во внешнем электрическом поле $\vec{E}$ равна \begin{equation}\label{F_dipole_eq1} \vec{F}=\left(\vec{d} \cdot \nabla \right)\vec{E}. \end{equation} Формула \eqref{F_dipole_eq1} применима как к твердому, так и к упругому $\left( \vec{d}(\vec{r}) \propto \vec{E}(\vec{r})\right)$ диполю.

В случае твердого диполя $$ \begin{array}{l} сила \; \vec{F}=\nabla \left(\vec{d} \cdot \vec{E}\right),\\\\ потенциальная \; энергия \; U=-\left(\vec{d} \cdot \vec{E}\right). \end{array} $$ В случае упругого диполя $$ \begin{array}{l} сила \; \vec{F}=\frac{1}{2}\nabla \left(\vec{d} \cdot \vec{E}\right),\\\\ потенциальная \; энергия \; U=-\frac{1}{2}\left(\vec{d} \cdot \vec{E}\right). \end{array} $$ Момент силы на электрический диполь с моментом $\vec{d}$ во внешнем электрическом поле $\vec{E}$ равен $$ \vec{N}=\left[\vec{d} \times \vec{E}\right]. $$

Задача №600
Найти силу, действующую на равномерно заряженное кольцо радиуса $b$ с зарядом $q$ со стороны маленького диэлектрического шарика радиуса $a$ с проницаемостью $\varepsilon$, расположенного на оси кольца на расстоянии $l$ от его центра. При этом считать, что $a\ll l,b$.

Показать решение

Задача №543
Два постоянных точечных диполя расположены в одной плоскости, как показано на рисунке. Во сколько раз изменится потенциальная энергия взаимодействия диполей, если один из диполей повернуть (см. рис.)? Угол $\alpha$, указанный на рисунке, равен 60$^{\circ}$.

Показать решение

Задача №542
Два постоянных точечных диполя расположены в одной плоскости, как показано на рисунке. Во сколько раз изменится потенциальная энергия взаимодействия диполей, если один из диполей повернуть (см. рис.)? Угол $\alpha$, указанный на рисунке, равен 45$^{\circ}$.

Показать решение

Задача №475
На большом расстоянии $L$ от бесконечной равномерно заряженной нити (линейная плотность заряда $\varkappa$) находится незаряженный металлический шар радиуса $R$ $(L \gg R)$. Найти силу, с которой шар действует на нить.

Показать решение

Задача №321
Точечный электрический диполь находится между двумя точечными зарядами $q_1$ и $q_2$ на расстоянии $r$ от каждого. Дипольный момент $\vec{d}$ ориентирован вдоль прямой, соединяющей точечные заряды. Найти силу, действующую на диполь.

Показать решение

Задача №133
Найти энергию взаимодействия и силу, действующую на малое заряженное по объему тело с квадрупольным моментом $Q_{ij}$ (полный заряд тела и его дипольный момент равны нулю) со стороны внешнего слабонеоднородного электрического поля $\vec{E}(\vec{r})$.

Показать решение

Задача №123
На расстоянии $l$ от центра заземленной проводящей сферы радиуса $a$ ($a<l$) расположен точечный диполь $\vec{p}=p\vec{e}_z$ (см. рис.). Найти силу $\vec{F}$, действующую на диполь. К отталкиванию или притяжению приводит эта сила?

Показать решение

Задача №94
На цилиндр длиной $l$, радиуса $R$ с диэлектрической проницаемостью $\varepsilon $ падает плоскополяризованная электромагнитная волна $\vec{E}=\vec{E}_0{\e}^{i(\vec{k}\vec{r}-\omega t)}$. Векторы $\vec{E}_{0}$ и $\vec{k}$ перпендикулярны оси цилиндра, $l\gg R$. Длина волны $\lambda \gg R\sqrt \varepsilon$, но сравнима с длиной цилиндра. Найти дифференциальное сечение рассеяния волны $\dif\sigma $/$\dif\Omega $ как функцию углов $\theta $ и $\alpha $ сферической системы координат, ось $z$ которой направлена вдоль вектора $\vec{E}_{0}$.

Показать решение

Задача №89
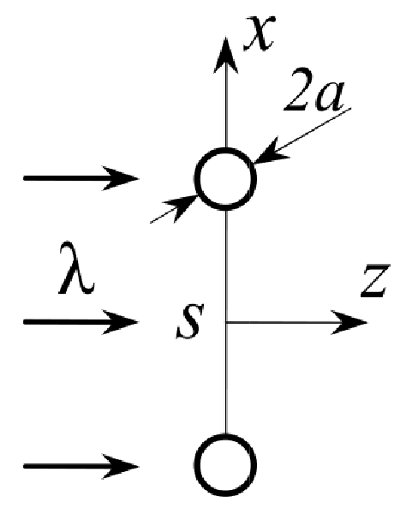
Два маленьких металлических шарика радиуса $a$ закреплены на оси $x$ на расстоянии $s$ друг от друга ($s\gg a$). На шарики вдоль оси $z$ падает плоская монохроматическая световая волна с длиной $\lambda\gg s$, линейно поляризованная по оси $x$. Измеряется интенсивность света, рассеянная шариками в направлении, противоположном оси $z$. Во сколько раз изменится ее величина, если шарики электрически соединить тонким проводником?

Показать решение

Задача №56
Шарик радиуса $a$ с диэлектрической проницаемостью $\varepsilon$ движется по прямой в направлении от неподвижного точечного заряда $Q$ с постоянной скоростью $v\ll c$. Найти энергию, излученную шариком на пути от начального положения (расстояние до заряда $R_{0}\gg a)$ до бесконечности.

Показать решение

Задача №55
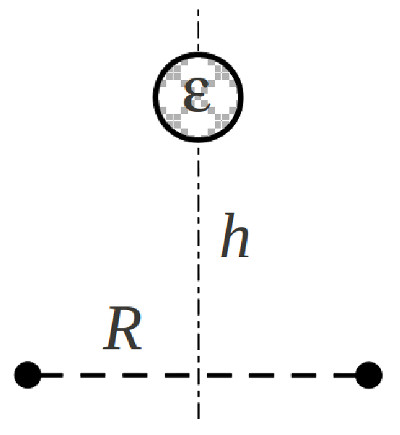
На оси симметрии тонкого кольца радиуса $R$, заряженного зарядом $q$, на расстоянии $h$ от его центра расположен диэлектрический шарик радиуса $a$ ($a\ll R$) с проницаемостью диэлектрика $\varepsilon $. Какая сила действует на шарик?

Показать решение

Задача №14
На расстоянии $a$ от полупространства, заполненного однородным диэлектриком с проницаемостью $\varepsilon $, закреплен центр точечного диполя с дипольным моментом $d$. Диполь может свободно вращаться, изменяя направление вектора $\vec{d}$. Параллельно границе полупространства приложено однородное внешнее электрическое поле $\vec{E}$. Найти установившееся равновесное значение угла $\alpha $ между направлением $\vec{E}$ и $\vec{d}$

Показать решение